1. 선택 정렬 ( Selection Sort )
선택된 값과 나머지 데이터를 비교하여 알맞는 자리를 찾는 알고리즘.
데이터 중 가장 작은 값의 데이터를 선택하여 앞으로 보내는 방법.
안정성 미보장.
시간복잡도는 O(N2)로 버블정렬과 같지만, 실제로 측정해보면 버블정렬에 비해 조금 더 빠르다.
public static void selectionSort(int[] arr){
for (int i = 0; i < arr.length; i++){
int minIndex = i;
for (int j = i; j < arr.length - 1; j++){
if(arr[j] < arr[minIndex]) minIndex = j;
}
int tmp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = tmp;
}
}
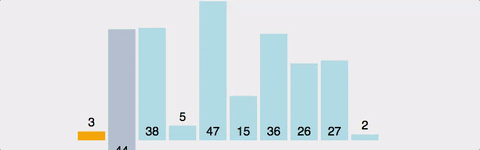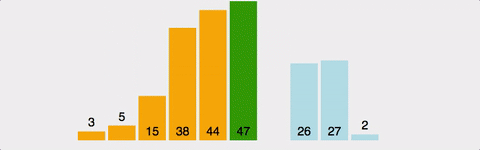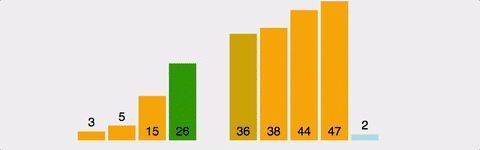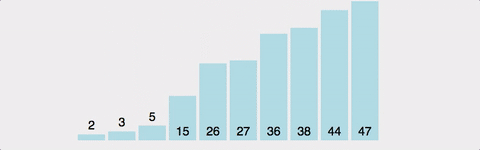
2. 삽입 정렬 ( Insertion Sort)
데이터들을 순회하면서 정렬이 필요한 요소를 뽑아내어 적당한 위치로 삽입하는 알고리즘.
두번째 데이터 부터 시작하여 그 앞의 데이터들과 비교하여 삽입할 위치를 정한 후 더 큰 데이터들을 뒤로 옮기고 그 위치에 데이터를 삽입한다.
버블솔트보다 성능이 좋다.
시간복잡도는 최선의 경우 O(N)이라는 매우 빠른 속도를 가지지만, 최악의 경우O(N2)이 된다.
public static void insertionSort(int[] arr){
for (int i = 1; i < arr.length; i++){
int target = arr[i];
int j = 0;
for (j = i - 1; j >= 0 && target < arr[j]; j--){
arr[j + 1] = arr[j];
}
arr[j + 1] = target;
}
}
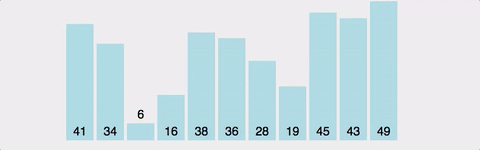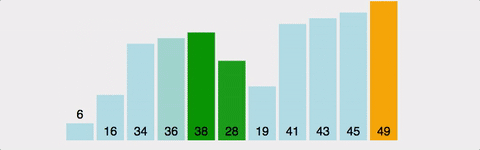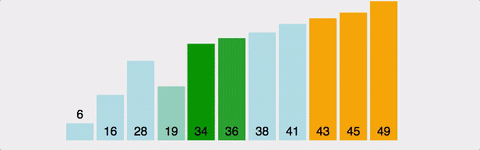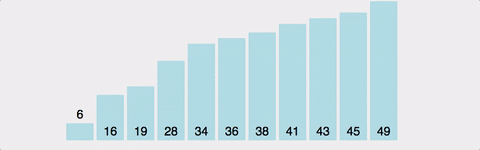
3. 버블 정렬 ( Bubble Sort )
인접한 두 수를 비교하여 정렬하는 알고리즘.
안정성 보장.
모든 정렬 중에 가장 느리다.
시간복잡도는 최선이든 최악이든 O(N2)
public static void bubbleSort(int[] arr){
for (int i = 0; i < arr.length; i++){
for (int j = 0; j < arr.length - 1; j++){
if(arr[j] > arr[j + 1]){
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
4. 병합 정렬 (Merge Sort)
2개 이상의 부분 배열로 분할하고 부분 배열에서 정렬을 한 뒤에 결합하여 다시 정렬을 진행한다.
분할(Divide), 정복(Conquer), 결합(Combine) 세개의 단계로 이루어져있다.
- 분할 : 배열을 부분 배열로 분할한다.
- 정복 : 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출을 이용하여 다시 분할 정복 방법을 적용한다.
- 결합 : 정렬된 부분 배열들을 하나의 배열에 합병한다.
매우 준수한 속도를 보여주지만, 추가적인 메모리가 필요하기 때문에 추가적인 메모리 할당이 가능할때 고려해 보는 것이 좋다.
시간 복잡도는 최선이든 최악이든 항상 O( NlogN ) 이다.

public static void mergeSort(int[] arr){
divide(arr, 0, arr.length - 1);
}
static void divide(int[] arr, int start, int end){
int mid = (start + end) / 2;
if (end - start > 0){
divide(arr, start, mid);
divide(arr, mid + 1, end);
conquer(arr, start, mid, end);
}
}
static void conquer(int[] arr, int start, int mid, int end) {
int point = 0, left = start, right = mid + 1 ;
int[] sorted = new int[end - start + 1];
while (left <= mid && right <= end){
if(arr[left] >= arr[right]) sorted[point++] = arr[right++];
else sorted[point++] = arr[left++];
}
while (right <= end){
sorted[point++] = arr[right++];
}
while (left <= mid){
sorted[point++] = arr[left++];
}
point = 0;
for (int i = start; i <= end; i++){
arr[i] = sorted[point++];
}
}
5. 퀵 정렬 (Quick Sort).
분할 정복 알고리즘의 하나로, 합병 정렬과 달리 리스트를 비균등하게 분할한다.
매우 빠른 수행 속도를 자랑하지만, 불안정 정렬에 속한다.
피벗을 기준으로 피벗보다 작은 요소들은 앞쪽으로, 큰 요소들은 뒷쪽으로 이동시킨다.
리스트를 한번 다 비교하면, 피벗을 작은 요소들 중 제일 뒤에있는 요소와 위치를 교환한 후
앞쪽과 뒷쪽을 분할하여 같은 방식으로 반복한다.
더이상 분할이 불가능하게 다 분할하고 나면 정렬이 다 되었다고 본다.
시간 복잡도는 최선의 경우 O(nlogn), 최악의 경우 O(n2) 이다.

static void sort(int[] arr, int start, int end, int[] sorted){
int pivot = arr[start];
int startIndex = start + 1, endIndex = end;
if(start < end){
while (startIndex < endIndex){
while (arr[startIndex] < pivot) startIndex++;
while (arr[endIndex] > pivot) endIndex--;
if(startIndex < endIndex){
int tmp = arr[startIndex];
arr[startIndex++] = arr[endIndex];
arr[endIndex--] = tmp;
}
}
startIndex--;
int tmp = arr[startIndex];
arr[startIndex] = arr[start];
arr[start] = tmp;
sorted[startIndex] = arr[startIndex];
if(startIndex - start > 0) sort(arr, start, startIndex - 1, sorted);
if(end - startIndex > 0) sort(arr, startIndex + 1, end, sorted);
}else{
sorted[start] = arr[start];
}
}
6. 기수 정렬 (Radix Sort)
다른 정렬들은 모두 데이터들을 비교하는 정렬 방식이었지만, 기수 정렬은 이와는 다르게 데이터들을 비교하지 않는다.
버킷을 이용한 정렬 방법으로, 낮은 자리에서 높은 자리순으로 버킷에 넣어 정렬한다.
매우 빠른 정렬 알고리즘이다.
데이터 전체 크기에 기수 테이블의 크기만한 메모리리가 더 필요하며, 정렬할 수 있는 데이터의 타입이 제한된다.
기수 정렬을 사용하기 위해서는 데이터들이 동일한 길이를 가지는 숫자나 문자열로 구성되어 있어야만 한다.
시간 복잡도는 O(dn) 이다.
static void radixSort(int[] arr){
// 0~9까지 넣을 버킷
Queue<Integer>[] bucket = new LinkedList[10];
for (int i = 0; i < 10; i++){
bucket[i] = new LinkedList<>();
}
int factor = 1;
for (int i = 0; i < 2; i++){
for (int j =0; j < arr.length; j++){
bucket[(arr[j] / factor) % 10].add(arr[j]);
}
int k = 0;
for (Queue<Integer> integers : bucket) {
while (!integers.isEmpty()){
arr[k++] = integers.poll();
}
}
factor *= 10;
}
}
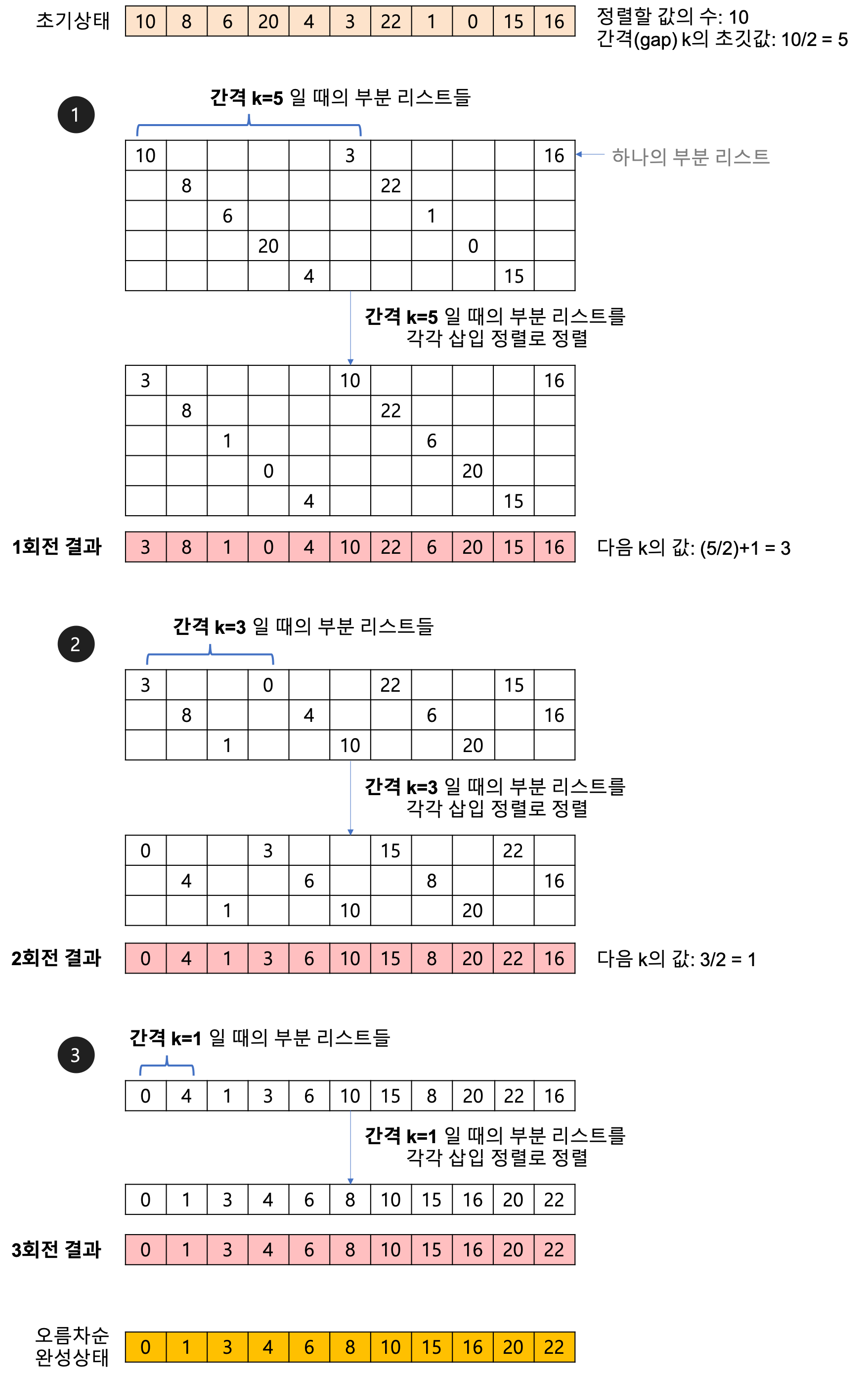
7. 셸 정렬 (ShellSort)
삽입 정렬을 보완하여 좀 더 빠르게 정렬하는 알고리즘.
정렬해야 할 리스트의 각 k 번째 요소를 추출하여 부분 리스트를 만든다.
이때, k를 간격(gap)이라 한다.
간격의 초기값 : 리스트의 길이 / 2
간격은 홀수로 하는 것이 성능에 더 도움이 되어, 짝수가 나오면 1을 더하여 홀수로 만든다.
홀수가 성능에 더 도움이 되는 이유는, 가격이 1이 되기전에 최대한 많이 부분 리스트에서 정렬을 해놔야 하기 때문입니다.
생성된 부분리스트의 개수는 gap과 같다.
시간 복잡도는 최선의 경우 O(n), 최악의 경우 O(n2) 이다.
static void shellSort(int[] arr){
for (int gap = arr.length / 2; gap > 0; gap /= 2){
if(gap%2 == 0) gap++;
//부분 배열의 개수 = gap
for (int i = 0; i < gap; i++){
//한 부분배열을 삽입정렬
for(int j = i + gap; j <= arr.length - 1; j += gap){
int target = arr[j];
int k;
for(k = j - gap; k >= i && arr[k] > target; k -= gap){
arr[k + gap] = arr[k];
}
arr[k + gap] = target;
}
}
}
}
8. 힙 정렬 ( Heap Sort)
최대, 최소 힙 트리를 구성해 정렬하는 방법.
내림차순 정렬을 위해서는 최대 힙, 오름차순 정렬을 위해서는 최소 힙을 구성하면 된다.

이미지 파일 출처
https://gmlwjd9405.github.io/
'Algorithm' 카테고리의 다른 글
| 동적 계획법 (Dynamic Programming) (0) | 2024.01.29 |
|---|---|
| 백트래킹 (Back Tracking) (0) | 2024.01.29 |
| 깊이 우선 탐색 (Depth-First Search) (0) | 2024.01.29 |
| 너비 우선 탐색 (Breadth-First Search) (0) | 2024.01.29 |
| 이진 탐색 (Binary Search) (0) | 2024.01.24 |
